Initial commit
This commit is contained in:
parent
6cdb771f66
commit
28ffcf80a0
90
README.md
90
README.md
|
|
@ -1,3 +1,89 @@
|
|||
# AT_chess
|
||||
# 基于α-β剪枝算法实现的AI五子棋游戏
|
||||
|
||||
基于α-β剪枝算法实现的AI五子棋游戏
|
||||
# 一、对抗问题
|
||||
|
||||
对抗问题:顾名思义,博弈双方是带有对抗性质的。博弈的任何一方都希望局面尽量对自己有利,同时局面也应该尽量令对方不利。通常这一类问题可以通过 Minimax 算法解决。
|
||||
|
||||
Minimax 算法又名极小化极大算法,是一种找出失败的最大可能性中的最小值的算法。Minimax 算法常用于棋类等由两方较量的游戏和程序,这类程序由两个游戏者轮流,每次执行一个步骤。为了执行 Minimax 算法,我们可以通过穷举的方式,枚举所有的状态空间,从而使得我们可以在游戏刚一开始,就预测到输赢。但是,在实际情况下,游戏的状态空间都是异常庞大的。很显然,我们不能将以穷举方式实现的 Minimax 算法用于实际应用。
|
||||
|
||||
# 二、α-β减枝
|
||||
|
||||
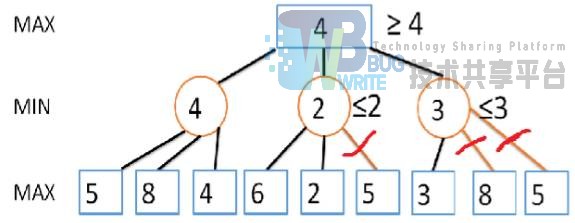
通过分析可以发现,在利用穷举方法执行 Minimax 算法中有许多的无效搜索,也就是说,许多明显较劣的状态分支我们也进行搜索了。我们在进行极大值搜索的时候,我们仅仅关心,下面最大的状态,对于任何小于目前值的分支也都是完全没有必要进行进一步检查的。(α减枝)
|
||||
|
||||
|
||||
|
||||
通过上图,我们可以发现,我们可以减去大量无用的状态检查,从而降低我们的运算量。
|
||||
|
||||
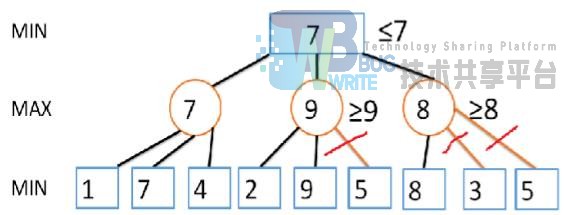
同时,我们在进行极小值搜索的时候,我们仅仅关心,下面最小的状态,对于任何大于目前值的分支都是完全没有必要进行进一步检查的。(β 减枝)
|
||||
|
||||
|
||||
|
||||
通过上图,我们可以发现,我们可以减去大量无用的状态检查,从而降低我们的运算量。
|
||||
|
||||
将上述所提到的 α 减枝与 β 减枝进行综合就可以得到 α-β 减枝。对于对抗搜索而言,我们需要精心设计其估值函数,不然我们的 α-β 减枝将毫无用武之地。
|
||||
|
||||
# 三、五子棋问题
|
||||
|
||||
五子棋:是一种两人对弈的纯策略型棋类游戏,通常双方分别使用黑白两色的棋子,下在棋盘直线与横线的交叉点上,先形成 5 子连线者获胜。
|
||||
|
||||

|
||||
|
||||
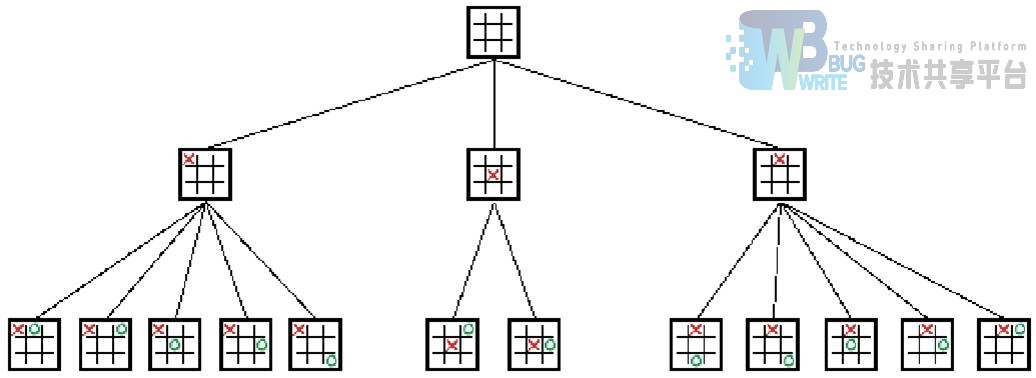
这里,我们采用了极大极小博弈树(MGT),来实现 AI。这里用一张井字棋的搜索示意图来说明。
|
||||
|
||||
|
||||
|
||||
上图很清晰的展示了对局可能出现的所有情况(已经去除了等价的情况),如果让这个图延展下去,我们就相当于穷举了所有的下法,如果我们能在知道所有下法的情况下,对这些下法加以判断,我们的 AI自然就可以选择具有最高获胜可能的位置来下棋。极大极小博弈树就是一种选择方法,由于五子棋以及大多数博弈类游戏是无法穷举出所有可能的步骤的(状态会随着博弈树的扩展而呈指数级增长),所以通常我们只会扩展有限的层数,而 AI 的智能高低,通常就会取决于能够扩展的层数,层数越高,AI 了解的信息就越多,就越能做出有利于它的判断。
|
||||
|
||||
为了让计算机选择那些获胜可能性高的步骤走,我们就需要一个对局面进行打分的算法,越有利,算法给出的分数越高。在得到这个算法过后,计算机就可以进行选择了,在极大极小博弈树上的选择规则是这样的:
|
||||
|
||||
- AI 会选择子树中具有最高估值叶子节点的路径
|
||||
|
||||
- USER 会选择子树中具有最小估值叶子节点的路径
|
||||
|
||||
这样的原则很容易理解,作为玩家,我所选择的子一定要使自己的利益最大化,而相应的在考虑对手的时候,也不要低估他,一定要假设他会走对他自己最有利,也就是对我最不利的那一步。
|
||||
|
||||
接下来,我们实现关键的局面评分步骤:直接分析整个棋面是一件很复杂的事情,为了让其具备可分析性,我们可以将其进行分解,分解成易于我们理解和实现的子问题。
|
||||
|
||||
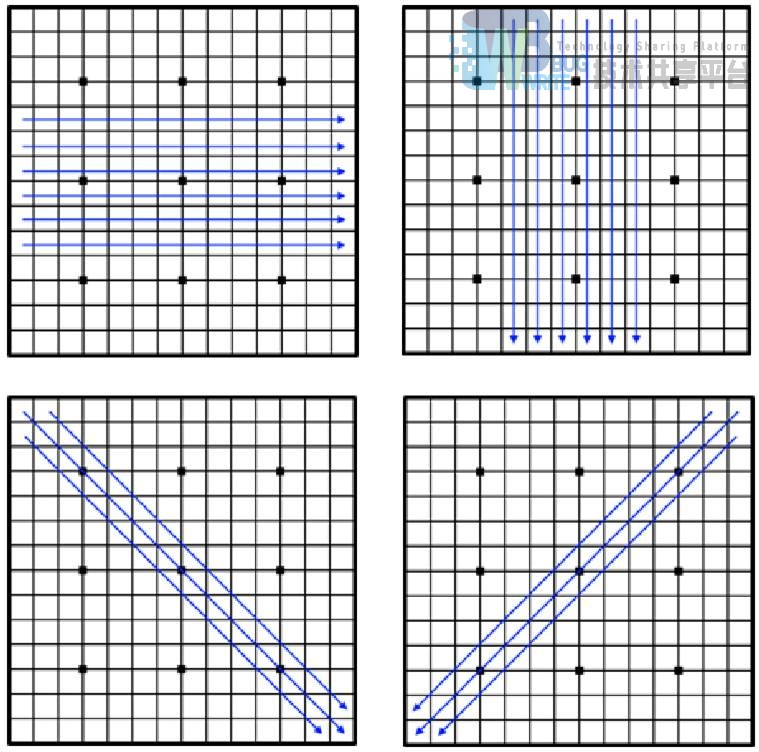
对于一个二维的期面,五子棋不同于围棋,五子棋的胜负只取决于一条线上的棋子,所以根据五子棋的这一特征,我们就来考虑将二维的棋面转换为一维的,下面是一种简单的思考方式,对于整个棋盘,我们只需要考虑四个方向即可,所以我们就按照四个方向来将棋盘转换为 15 * 6 个长度不超过 15 的一维向量(分解斜向的时候,需要分为上下两个半区),参考下图:
|
||||
|
||||
|
||||
|
||||
我们的目的是为了为其评分,那么我们就还需要评估每个线状态,将每个线状态的评分进行汇总,当做我们的棋面评分:
|
||||
|
||||

|
||||
|
||||
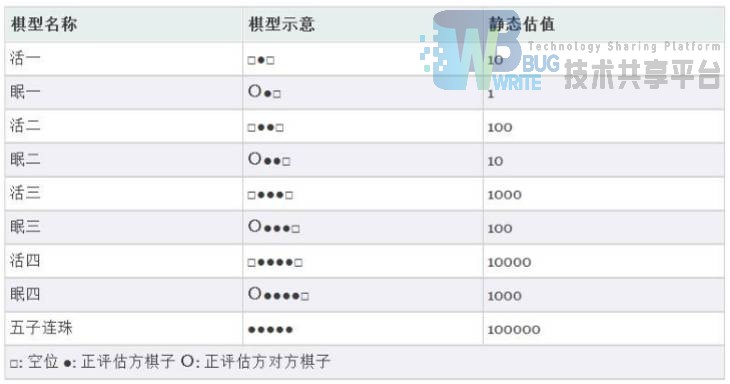
接下来我们所要做的就是评价每一条线状态,根据五子棋的规则,我们可以很容易穷举出各种可能出现的基本棋型,我们首先为这些基本棋型进行识别和评价,并且统计每个线状态中出现了多少种下面所述的棋型,并据此得出评价值,得到如下图所示的静态估值表:
|
||||
|
||||
|
||||
|
||||
根据这个表以及我们之前所谈到的规则,我们就可以得到一个可以运行的AI了。
|
||||
|
||||
# 四、进一步的优化
|
||||
|
||||
注意到,如果我们搜索到第四层,总共需要搜索:224 + 224 * 223 + 224 * 223 * 222 + 224 * 223 * 222 * 221 = 2 461 884 544 个状态节点,搜索如此多的状态节点的开销是十分可观的,因此,我们提高效率的方式就锁定到了:如何减少需要搜索的状态节点。
|
||||
|
||||
我们可以采取以下方法来减少需要搜索的状态节点:
|
||||
|
||||
- 我们可以利用经典的α-β剪枝算法对博弈树剪枝
|
||||
|
||||
- 我们可以每次搜索仅搜索落子点周围 2\*2 格范围内存在棋子的位置,这样可以避免搜索一些明显无用的节点,而且可以大幅度提升整体搜索速度
|
||||
|
||||
- 避免对必胜/负局面搜索,当搜索过程中出现了必胜/负局面的时候直接返回不再搜索,因为此时继续搜索是没有必要的,直接返回当前棋局的估价值即可
|
||||
|
||||
- 加入随机化AI的下棋方式,普通的AI算法对于给定的玩家下棋方式会给出固定的回应,这就导致玩家获胜一次之后只要此后每次都按此方式下棋,都能够获胜。为了避免这种情况,可以在 AI选择下子位置的时候,在估值相差不多的几个位置中随机挑选一个进行放置,以此增加 AI的灵活性
|
||||
|
||||
规划搜索顺序,有很多有价值的下子点存在于更靠近棋盘中央的地方,如果从棋盘中央向外搜索的话,则能够提高α-β剪枝的效率,让尽可能多的分支被排除
|
||||
|
||||
# 五、实验成果
|
||||
|
||||
|
||||
|
||||

|
||||
|
||||
# 六、实验总结
|
||||
|
||||
通过本次实验,加强了组员之间的沟通协调能力,同时也提高了我们对αβ减枝算法的了解。我们更了解了五子棋相关的游戏规则以及一些技巧,拓宽了我们的知识面,有助于我们在未来的生活中更好的与人交流。
|
||||
|
||||
同时,经过此次实验,我们深入了解了棋类人工智能算法,进一步的提升了我们的专业水平,有助于我们在未来的就业与科研岗位上走的更远。
|
||||
|
||||
虽然α-β减枝实现起来非常容易,但是五子棋的局势估计却十分的有挑战性,其局势估计的准确与否直接影响了程序的运行结果是否令人满意,AI是否能够展现出足够的智能。
|
||||
|
|
@ -0,0 +1,17 @@
|
|||
# Auto detect text files and perform LF normalization
|
||||
* text=auto
|
||||
|
||||
# Custom for Visual Studio
|
||||
*.cs diff=csharp
|
||||
|
||||
# Standard to msysgit
|
||||
*.doc diff=astextplain
|
||||
*.DOC diff=astextplain
|
||||
*.docx diff=astextplain
|
||||
*.DOCX diff=astextplain
|
||||
*.dot diff=astextplain
|
||||
*.DOT diff=astextplain
|
||||
*.pdf diff=astextplain
|
||||
*.PDF diff=astextplain
|
||||
*.rtf diff=astextplain
|
||||
*.RTF diff=astextplain
|
||||
|
|
@ -0,0 +1,605 @@
|
|||
#include "opencv2/imgproc/imgproc.hpp"
|
||||
#include "opencv2/imgcodecs.hpp"
|
||||
#include "opencv2/videoio/videoio.hpp"
|
||||
#include "opencv2/highgui/highgui.hpp"
|
||||
|
||||
#include <iostream>
|
||||
|
||||
#include <iostream>
|
||||
#include <cstdio>
|
||||
#include <cstring>
|
||||
#include <cstdio>
|
||||
#include <cstdlib>
|
||||
#include <iomanip>
|
||||
|
||||
using namespace std;
|
||||
using namespace cv;
|
||||
//sro 菜神 Orz
|
||||
|
||||
cv::Mat chessboard, whiteChess, blackChess, tmp, BGS;
|
||||
|
||||
int is_red(Vec3b X) {
|
||||
// cout << (int)X[1] << ' ' << (int)X[2] << ' ' << (int)X[3] << endl;
|
||||
return X[0] < 200 && X[1] < 200 && X[2] > 230;
|
||||
}
|
||||
|
||||
cv::Mat BG;
|
||||
|
||||
void imageCopyToBG(cv::Mat chess, int x, int y) {
|
||||
x *= 35;
|
||||
y *= 35;
|
||||
int rows = chess.rows;
|
||||
int cols = chess.cols;
|
||||
for (int i = 0; i < rows; ++i) {
|
||||
for (int j = 0; j < cols; ++j) {
|
||||
if (!is_red(chess.at<Vec3b>(i, j))) {
|
||||
BG.at<Vec3b>(x + i + 8, y + j + 8) = chess.at<Vec3b>(i, j);
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
实现用的参数
|
||||
*/
|
||||
class CONFIG {
|
||||
public:
|
||||
static const int BOARD_SIZE = 15;
|
||||
static const int EMPTY = 0;
|
||||
static const int USER_1 = 1;
|
||||
static const int USER_2 = 2;
|
||||
static const int AI_EMPTY = 0; // 无子
|
||||
static const int AI_MY = 1; // 待评价子
|
||||
static const int AI_OP = 2; // 对方子或不能下子
|
||||
static const int MAX_NODE = 2;
|
||||
static const int MIN_NODE = 1;
|
||||
static const int INF = 106666666;
|
||||
static const int ERROR_INDEX = -1;
|
||||
//估价值
|
||||
static const int AI_ZERO = 0;
|
||||
static const int AI_ONE = 10;
|
||||
static const int AI_ONE_S = 1;
|
||||
static const int AI_TWO = 100;
|
||||
static const int AI_TWO_S = 10;
|
||||
static const int AI_THREE = 1000;
|
||||
static const int AI_THREE_S = 100;
|
||||
static const int AI_FOUR = 10000;
|
||||
static const int AI_FOUR_S = 1000;
|
||||
static const int AI_FIVE = 100000;
|
||||
};
|
||||
|
||||
/*
|
||||
棋盘格子
|
||||
*/
|
||||
class Grid :CONFIG {
|
||||
public:
|
||||
int type; //类型
|
||||
|
||||
Grid() {
|
||||
type = EMPTY;
|
||||
}
|
||||
|
||||
Grid(int t) {
|
||||
type = t;
|
||||
}
|
||||
|
||||
void grid(int t = EMPTY) {
|
||||
type = t;
|
||||
}
|
||||
|
||||
int isEmpty() {
|
||||
return type == EMPTY ? true : false;
|
||||
}
|
||||
};
|
||||
|
||||
/*
|
||||
棋盘
|
||||
*/
|
||||
class ChessBoard :CONFIG {
|
||||
public:
|
||||
Grid chessBoard[BOARD_SIZE][BOARD_SIZE];
|
||||
|
||||
ChessBoard() {
|
||||
for (int i = 0; i < BOARD_SIZE; ++i)
|
||||
for (int j = 0; j < BOARD_SIZE; ++j)
|
||||
chessBoard[i][j].grid();
|
||||
}
|
||||
|
||||
ChessBoard(const ChessBoard &othr) {
|
||||
for (int i = 0; i < BOARD_SIZE; ++i)
|
||||
for (int j = 0; j < BOARD_SIZE; ++j)
|
||||
chessBoard[i][j].grid(othr.chessBoard[i][j].type);
|
||||
}
|
||||
|
||||
/*
|
||||
放置棋子
|
||||
返回放置棋子是否成功
|
||||
*/
|
||||
bool placePiece(int x, int y, int type) {
|
||||
if (chessBoard[x][y].isEmpty()) {
|
||||
chessBoard[x][y].type = type;
|
||||
return true;
|
||||
}
|
||||
return false;
|
||||
}
|
||||
};
|
||||
|
||||
/*
|
||||
煞笔AI
|
||||
*/
|
||||
class Game :CONFIG {
|
||||
public:
|
||||
ChessBoard curState; // 当前棋盘
|
||||
bool isStart; // 是否进行中
|
||||
int curUser; // 当前行棋人
|
||||
int MAX_DEPTH; // 最大搜索层数
|
||||
|
||||
/*
|
||||
开始并设定难度
|
||||
*/
|
||||
void startGame(int nd = 2) {
|
||||
MAX_DEPTH = nd;
|
||||
isStart = true;
|
||||
curUser = USER_1;
|
||||
}
|
||||
|
||||
/*
|
||||
转换行棋人
|
||||
*/
|
||||
void changeUser() {
|
||||
curUser = curUser == USER_1 ? USER_2 : USER_1;
|
||||
}
|
||||
|
||||
/*
|
||||
根据给定type
|
||||
A:待判断棋子的类型
|
||||
type:我方棋子的类型
|
||||
返回A是待判断棋子 无棋子 对方棋子
|
||||
*/
|
||||
int getPieceType(int A, int type) {
|
||||
return A == type ? AI_MY : (A == EMPTY ? AI_EMPTY : AI_OP);
|
||||
}
|
||||
|
||||
int getPieceType(const ChessBoard &board, int x, int y, int type) {
|
||||
if (x < 0 || y < 0 || x >= BOARD_SIZE || y >= BOARD_SIZE)// 超出边界按对方棋子算
|
||||
return AI_OP;
|
||||
else
|
||||
return getPieceType(board.chessBoard[x][y].type, type);
|
||||
}
|
||||
|
||||
/*
|
||||
当前行棋人放置棋子
|
||||
放置失败返回失败
|
||||
放置成功
|
||||
检察游戏是否结束
|
||||
转换游戏角色后返回成功
|
||||
*/
|
||||
bool placePiece(int x, int y) {
|
||||
if (curState.placePiece(x, y, curUser)) {
|
||||
// 检察行棋人是否胜利
|
||||
if (isWin(x, y)) {
|
||||
isStart = false; // 游戏结束
|
||||
// return true;
|
||||
}
|
||||
changeUser(); // 转换游戏角色
|
||||
return true;
|
||||
}
|
||||
return false;
|
||||
}
|
||||
|
||||
bool isWin(int x, int y) {
|
||||
if (evaluatePiece(curState, x, y, curUser) >= AI_FIVE)
|
||||
return true;
|
||||
return false;
|
||||
}
|
||||
|
||||
/*
|
||||
以center作为评估位置进行评价一个方向的棋子
|
||||
*/
|
||||
int evaluateLine(int line[], bool ALL) {
|
||||
int value = 0; // 估值
|
||||
int cnt = 0; // 连子数
|
||||
int blk = 0; // 封闭数
|
||||
for (int i = 0; i < BOARD_SIZE; ++i) {
|
||||
if (line[i] == AI_MY) { // 找到第一个己方的棋子
|
||||
// 还原计数
|
||||
cnt = 1;
|
||||
blk = 0;
|
||||
// 看左侧是否封闭
|
||||
if (line[i - 1] == AI_OP)
|
||||
++blk;
|
||||
// 计算连子数
|
||||
for (i = i + 1; i < BOARD_SIZE && line[i] == AI_MY; ++i, ++cnt);
|
||||
// 看右侧是否封闭
|
||||
if (line[i] == AI_OP)
|
||||
++blk;
|
||||
// 计算评估值
|
||||
value += getValue(cnt, blk);
|
||||
}
|
||||
}
|
||||
return value;
|
||||
}
|
||||
|
||||
/*
|
||||
以center作为评估位置进行评价一个方向的棋子(前后4格范围内)
|
||||
*/
|
||||
int evaluateLine(int line[]) {
|
||||
int cnt = 1; // 连子数
|
||||
int blk = 0; // 封闭数
|
||||
// 向左右扫
|
||||
for (int i = 3; i >= 0; --i) {
|
||||
if (line[i] == AI_MY) ++cnt;
|
||||
else if (line[i] == AI_OP) {
|
||||
++blk;
|
||||
break;
|
||||
}
|
||||
else
|
||||
break;
|
||||
}
|
||||
for (int i = 5; i < 9; ++i) {
|
||||
if (line[i] == AI_MY) ++cnt;
|
||||
else if (line[i] == AI_OP) {
|
||||
++blk;
|
||||
break;
|
||||
}
|
||||
else
|
||||
break;
|
||||
}
|
||||
return getValue(cnt, blk);
|
||||
}
|
||||
|
||||
/*
|
||||
根据连字数和封堵数给出一个评价值
|
||||
*/
|
||||
int getValue(int cnt, int blk) {
|
||||
if (blk == 0) {// 活棋
|
||||
switch (cnt) {
|
||||
case 1:
|
||||
return AI_ONE;
|
||||
case 2:
|
||||
return AI_TWO;
|
||||
case 3:
|
||||
return AI_THREE;
|
||||
case 4:
|
||||
return AI_FOUR;
|
||||
default:
|
||||
return AI_FIVE;
|
||||
}
|
||||
}
|
||||
else if (blk == 1) {// 单向封死
|
||||
switch (cnt) {
|
||||
case 1:
|
||||
return AI_ONE_S;
|
||||
case 2:
|
||||
return AI_TWO_S;
|
||||
case 3:
|
||||
return AI_THREE_S;
|
||||
case 4:
|
||||
return AI_FOUR_S;
|
||||
default:
|
||||
return AI_FIVE;
|
||||
}
|
||||
}
|
||||
else {// 双向堵死
|
||||
if (cnt >= 5)
|
||||
return AI_FIVE;
|
||||
else
|
||||
return AI_ZERO;
|
||||
}
|
||||
}
|
||||
|
||||
/*
|
||||
对一个状态的一个位置放置一种类型的棋子的优劣进行估价
|
||||
*/
|
||||
int evaluatePiece(ChessBoard state, int x, int y, int type) {
|
||||
int value = 0; // 估价值
|
||||
int line[17]; //线状态
|
||||
bool flagX[8];// 横向边界标志
|
||||
flagX[0] = x - 4 < 0;
|
||||
flagX[1] = x - 3 < 0;
|
||||
flagX[2] = x - 2 < 0;
|
||||
flagX[3] = x - 1 < 0;
|
||||
flagX[4] = x + 1 > 14;
|
||||
flagX[5] = x + 2 > 14;
|
||||
flagX[6] = x + 3 > 14;
|
||||
flagX[7] = x + 4 > 14;
|
||||
bool flagY[8];// 纵向边界标志
|
||||
flagY[0] = y - 4 < 0;
|
||||
flagY[1] = y - 3 < 0;
|
||||
flagY[2] = y - 2 < 0;
|
||||
flagY[3] = y - 1 < 0;
|
||||
flagY[4] = y + 1 > 14;
|
||||
flagY[5] = y + 2 > 14;
|
||||
flagY[6] = y + 3 > 14;
|
||||
flagY[7] = y + 4 > 14;
|
||||
|
||||
line[4] = AI_MY; // 中心棋子
|
||||
// 横
|
||||
line[0] = flagX[0] ? AI_OP : (getPieceType(state.chessBoard[x - 4][y].type, type));
|
||||
line[1] = flagX[1] ? AI_OP : (getPieceType(state.chessBoard[x - 3][y].type, type));
|
||||
line[2] = flagX[2] ? AI_OP : (getPieceType(state.chessBoard[x - 2][y].type, type));
|
||||
line[3] = flagX[3] ? AI_OP : (getPieceType(state.chessBoard[x - 1][y].type, type));
|
||||
|
||||
line[5] = flagX[4] ? AI_OP : (getPieceType(state.chessBoard[x + 1][y].type, type));
|
||||
line[6] = flagX[5] ? AI_OP : (getPieceType(state.chessBoard[x + 2][y].type, type));
|
||||
line[7] = flagX[6] ? AI_OP : (getPieceType(state.chessBoard[x + 3][y].type, type));
|
||||
line[8] = flagX[7] ? AI_OP : (getPieceType(state.chessBoard[x + 4][y].type, type));
|
||||
|
||||
value += evaluateLine(line);
|
||||
|
||||
// 纵
|
||||
line[0] = flagY[0] ? AI_OP : getPieceType(state.chessBoard[x][y - 4].type, type);
|
||||
line[1] = flagY[1] ? AI_OP : getPieceType(state.chessBoard[x][y - 3].type, type);
|
||||
line[2] = flagY[2] ? AI_OP : getPieceType(state.chessBoard[x][y - 2].type, type);
|
||||
line[3] = flagY[3] ? AI_OP : getPieceType(state.chessBoard[x][y - 1].type, type);
|
||||
|
||||
line[5] = flagY[4] ? AI_OP : getPieceType(state.chessBoard[x][y + 1].type, type);
|
||||
line[6] = flagY[5] ? AI_OP : getPieceType(state.chessBoard[x][y + 2].type, type);
|
||||
line[7] = flagY[6] ? AI_OP : getPieceType(state.chessBoard[x][y + 3].type, type);
|
||||
line[8] = flagY[7] ? AI_OP : getPieceType(state.chessBoard[x][y + 4].type, type);
|
||||
|
||||
value += evaluateLine(line);
|
||||
|
||||
// 左上-右下
|
||||
line[0] = flagX[0] || flagY[0] ? AI_OP : getPieceType(state.chessBoard[x - 4][y - 4].type, type);
|
||||
line[1] = flagX[1] || flagY[1] ? AI_OP : getPieceType(state.chessBoard[x - 3][y - 3].type, type);
|
||||
line[2] = flagX[2] || flagY[2] ? AI_OP : getPieceType(state.chessBoard[x - 2][y - 2].type, type);
|
||||
line[3] = flagX[3] || flagY[3] ? AI_OP : getPieceType(state.chessBoard[x - 1][y - 1].type, type);
|
||||
|
||||
line[5] = flagX[4] || flagY[4] ? AI_OP : getPieceType(state.chessBoard[x + 1][y + 1].type, type);
|
||||
line[6] = flagX[5] || flagY[5] ? AI_OP : getPieceType(state.chessBoard[x + 2][y + 2].type, type);
|
||||
line[7] = flagX[6] || flagY[6] ? AI_OP : getPieceType(state.chessBoard[x + 3][y + 3].type, type);
|
||||
line[8] = flagX[7] || flagY[7] ? AI_OP : getPieceType(state.chessBoard[x + 4][y + 4].type, type);
|
||||
|
||||
value += evaluateLine(line);
|
||||
|
||||
// 右上-左下
|
||||
line[0] = flagX[7] || flagY[0] ? AI_OP : getPieceType(state.chessBoard[x + 4][y - 4].type, type);
|
||||
line[1] = flagX[6] || flagY[1] ? AI_OP : getPieceType(state.chessBoard[x + 3][y - 3].type, type);
|
||||
line[2] = flagX[5] || flagY[2] ? AI_OP : getPieceType(state.chessBoard[x + 2][y - 2].type, type);
|
||||
line[3] = flagX[4] || flagY[3] ? AI_OP : getPieceType(state.chessBoard[x + 1][y - 1].type, type);
|
||||
|
||||
line[5] = flagX[3] || flagY[4] ? AI_OP : getPieceType(state.chessBoard[x - 1][y + 1].type, type);
|
||||
line[6] = flagX[2] || flagY[5] ? AI_OP : getPieceType(state.chessBoard[x - 2][y + 2].type, type);
|
||||
line[7] = flagX[1] || flagY[6] ? AI_OP : getPieceType(state.chessBoard[x - 3][y + 3].type, type);
|
||||
line[8] = flagX[0] || flagY[7] ? AI_OP : getPieceType(state.chessBoard[x - 4][y + 4].type, type);
|
||||
|
||||
value += evaluateLine(line);
|
||||
|
||||
return value;
|
||||
}
|
||||
|
||||
/*
|
||||
评价一个棋面上的一方
|
||||
*/
|
||||
int evaluateState(ChessBoard state, int type) {
|
||||
int value = 0;
|
||||
// 分解成线状态
|
||||
int line[6][17];
|
||||
int lineP;
|
||||
|
||||
for (int p = 0; p < 6; ++p)
|
||||
line[p][0] = line[p][16] = AI_OP;
|
||||
|
||||
// 从四个方向产生
|
||||
for (int i = 0; i < BOARD_SIZE; ++i) {
|
||||
// 产生线状态
|
||||
lineP = 1;
|
||||
|
||||
for (int j = 0; j < BOARD_SIZE; ++j) {
|
||||
line[0][lineP] = getPieceType(state, i, j, type); /* | */
|
||||
line[1][lineP] = getPieceType(state, j, i, type); /* - */
|
||||
line[2][lineP] = getPieceType(state, i + j, j, type); /* \ */
|
||||
line[3][lineP] = getPieceType(state, i - j, j, type); /* / */
|
||||
line[4][lineP] = getPieceType(state, j, i + j, type); /* \ */
|
||||
line[5][lineP] = getPieceType(state, BOARD_SIZE - j - 1, i + j, type); /* / */
|
||||
++lineP;
|
||||
}
|
||||
// 估计
|
||||
int special = i == 0 ? 4 : 6;
|
||||
for (int p = 0; p < special; ++p) {
|
||||
value += evaluateLine(line[p], true);
|
||||
}
|
||||
}
|
||||
return value;
|
||||
}
|
||||
|
||||
/*
|
||||
若x, y位置周围1格内有棋子则搜索
|
||||
*/
|
||||
bool canSearch(ChessBoard state, int x, int y) {
|
||||
|
||||
int tmpx = x - 1;
|
||||
int tmpy = y - 1;
|
||||
for (int i = 0; tmpx < BOARD_SIZE && i < 3; ++tmpx, ++i) {
|
||||
int ty = tmpy;
|
||||
for (int j = 0; ty < BOARD_SIZE && j < 3; ++ty, ++j) {
|
||||
if (tmpx >= 0 && ty >= 0 && state.chessBoard[tmpx][ty].type != EMPTY)
|
||||
return true;
|
||||
else
|
||||
continue;
|
||||
}
|
||||
}
|
||||
return false;
|
||||
}
|
||||
|
||||
/*
|
||||
给出后继节点的类型
|
||||
*/
|
||||
int nextType(int type) {
|
||||
return type == MAX_NODE ? MIN_NODE : MAX_NODE;
|
||||
}
|
||||
|
||||
/*
|
||||
state 待转换的状态
|
||||
type 当前层的标记:MAX MIN
|
||||
depth 当前层深
|
||||
alpha 父层alpha值
|
||||
beta 父层beta值
|
||||
*/
|
||||
int minMax(ChessBoard state, int x, int y, int type, int depth, int alpha, int beta) {
|
||||
ChessBoard newState(state);
|
||||
newState.placePiece(x, y, nextType(type));
|
||||
|
||||
int weight = 0;
|
||||
int max = -INF; // 下层权值上界
|
||||
int min = INF; // 下层权值下界
|
||||
|
||||
if (depth < MAX_DEPTH) {
|
||||
// 已输或已胜则不继续搜索
|
||||
if (evaluatePiece(newState, x, y, nextType(type)) >= AI_FIVE) {
|
||||
if (type == MIN_NODE)
|
||||
return AI_FIVE; // 我方胜
|
||||
else
|
||||
return -AI_FIVE;
|
||||
}
|
||||
|
||||
int i, j;
|
||||
for (i = 0; i < BOARD_SIZE; ++i) {
|
||||
for (j = 0; j < BOARD_SIZE; ++j) {
|
||||
if (newState.chessBoard[i][j].type == EMPTY && canSearch(newState, i, j)) {
|
||||
weight = minMax(newState, i, j, nextType(type), depth + 1, min, max);
|
||||
|
||||
if (weight > max)
|
||||
max = weight; // 更新下层上界
|
||||
if (weight < min)
|
||||
min = weight; // 更新下层下界
|
||||
|
||||
// alpha-beta
|
||||
if (type == MAX_NODE) {
|
||||
if (max >= alpha)
|
||||
return max;
|
||||
}
|
||||
else {
|
||||
if (min <= beta)
|
||||
return min;
|
||||
}
|
||||
}
|
||||
else
|
||||
continue;
|
||||
}
|
||||
}
|
||||
|
||||
if (type == MAX_NODE)
|
||||
return max; // 最大层给出最大值
|
||||
else
|
||||
return min; // 最小层给出最小值
|
||||
}
|
||||
else {
|
||||
weight = evaluateState(newState, MAX_NODE); // 评估我方局面
|
||||
weight -= type == MIN_NODE ? evaluateState(newState, MIN_NODE) * 10 : evaluateState(newState, MIN_NODE); // 评估对方局面
|
||||
return weight; // 搜索到限定层后给出权值
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
int cnt[BOARD_SIZE][BOARD_SIZE];
|
||||
/*
|
||||
AI 行棋
|
||||
*/
|
||||
bool placePieceAI() {
|
||||
int weight;
|
||||
int max = -INF; // 本层的权值上界
|
||||
int x = 0, y = 0;
|
||||
memset(cnt, 0, sizeof(cnt));
|
||||
for (int i = 0; i < BOARD_SIZE; ++i) {
|
||||
for (int j = 0; j < BOARD_SIZE; ++j) {
|
||||
if (curState.chessBoard[i][j].type == EMPTY && canSearch(curState, i, j)) {
|
||||
weight = minMax(curState, i, j, nextType(MAX_NODE), 1, -INF, max);
|
||||
cnt[i][j] = weight;
|
||||
if (weight > max) {
|
||||
max = weight; // 更新下层上界
|
||||
x = i;
|
||||
y = j;
|
||||
}
|
||||
}
|
||||
else
|
||||
continue;
|
||||
}
|
||||
}
|
||||
return placePiece(x, y); // AI最优点
|
||||
}
|
||||
|
||||
/*
|
||||
控制台打印。。。
|
||||
*/
|
||||
void show() {
|
||||
|
||||
chessboard.copyTo(BG);
|
||||
for (int i = 0; i < BOARD_SIZE; ++i) {
|
||||
for (int j = 0; j < BOARD_SIZE; ++j) {
|
||||
if (curState.chessBoard[i][j].type == 1)
|
||||
imageCopyToBG(blackChess, i, j);
|
||||
if (curState.chessBoard[i][j].type == 2)
|
||||
imageCopyToBG(whiteChess, i, j);
|
||||
}
|
||||
}
|
||||
for (int i = 0; i < BOARD_SIZE; ++i) {
|
||||
for (int j = 0; j < BOARD_SIZE; ++j) {
|
||||
if (curState.chessBoard[i][j].type == 0)
|
||||
cout << " -";
|
||||
if (curState.chessBoard[i][j].type == 1)
|
||||
cout << " X";
|
||||
if (curState.chessBoard[i][j].type == 2)
|
||||
cout << " O";
|
||||
}
|
||||
cout << endl;
|
||||
}
|
||||
imshow("gobang", BG);
|
||||
cv::waitKey(5);
|
||||
}
|
||||
|
||||
};
|
||||
|
||||
using namespace cv;
|
||||
using namespace std;
|
||||
|
||||
int X, Y = 0;
|
||||
int optIsOk = 1;
|
||||
Game G;
|
||||
|
||||
static void onMouse(int event, int x, int y, int, void*)
|
||||
{
|
||||
if (event != EVENT_LBUTTONDOWN)
|
||||
return;
|
||||
if (!optIsOk) return;
|
||||
X = x; Y = y;
|
||||
optIsOk = 0;
|
||||
}
|
||||
|
||||
int main(int argc, char** argv)
|
||||
{
|
||||
chessboard = cv::imread("chessboard.bmp");
|
||||
tmp = cv::imread("whiteChess.bmp");
|
||||
resize(tmp, whiteChess, Size(30, 30), 0, 0, CV_INTER_LINEAR);
|
||||
tmp = cv::imread("blackChess.bmp");
|
||||
resize(tmp, blackChess, Size(30, 30), 0, 0, CV_INTER_LINEAR);
|
||||
|
||||
namedWindow("gobang", 1);
|
||||
setMouseCallback("gobang", onMouse, 0);
|
||||
chessboard.copyTo(BG);
|
||||
imshow("gobang", BG);
|
||||
cv::waitKey(50);
|
||||
|
||||
int flag = 0;
|
||||
|
||||
G.startGame(4);
|
||||
for (;;)
|
||||
{
|
||||
// if (!optIsOk) {
|
||||
/* int tx = (X - 8) / 35, ty = (Y - 8) / 35;
|
||||
cout << tx << ' ' << ty << endl;
|
||||
G.placePiece(ty, tx);
|
||||
cout << tx << ' ' << ty << endl;*/
|
||||
G.placePieceAI();
|
||||
G.show();
|
||||
G.placePieceAI();
|
||||
G.show();
|
||||
optIsOk = 1;
|
||||
// }
|
||||
cv::waitKey(5);
|
||||
}
|
||||
|
||||
return 0;
|
||||
}
|
||||
Binary file not shown.
Loading…
Reference in New Issue